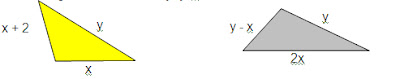https://www.box.com/s/f157af9c2ee2d340e09e
DESCARGAR ARCHIVO E IMPRIMIR
domingo, 4 de noviembre de 2012
domingo, 26 de agosto de 2012
domingo, 6 de mayo de 2012
ACTIVIDADES DEL QUINTO BLOQUE DE SEGUNDO GRADO DE MATEMÁTICASO DE MATEMÁTICAS
ACTIVIDADES DEL QUINTO BLOQUE DE SEGUNDO GRADO DE MATEMÁTICAS
8.5.1 Tema 1.- SISTEMAS DE ECUACIONES CON COEFICIENTES ENTEROS.
Alejandra y Erica fueron al cine y compraron dos helados
sencillos de chocolate y un refresco en vaso grande por $ 35.00. Si se sabe que
el precio del refresco en vaso grande vale la mitad del precio de un helado
sencillo de chocolate, ¿cuál es el precio de un helado de chocolate y cuál el
de un refresco en vaso grande?
Problema: a) El perímetro del
primer triangulo es 21 y el del segundo 23 ¿Cuánto valen “x” y “y”?.
8.5.1 Tema 1.- SISTEMAS DE ECUACIONES CON COEFICIENTES ENTEROS.
ACTIVIDAD 1: Organizados en equipos, resuelvan los
siguientes problemas:
- Una bolsa contiene en total 21 frutas,
de las cuales algunas son peras y otras son duraznos. ¿Cuántas peras y
cuántos duraznos hay en la bolsa?
- Si la cantidad de peras que hay en la
bolsa es 11 unidades más que la cantidad de duraznos, ¿cuántas peras y
cuántos duraznos hay en la bolsa?
ACTIVIDAD 2: Reunidos en equipos, resuelvan el siguiente
problema:
Problema: En la cooperativa escolar se vendieron 296
refrescos en total. Si los refrescos chicos vendidos fueron el triple de los
medianos. ¿Cuántos se vendieron de cada uno?
ACTIVIDAD 3: Consigna 1. Organizados en equipos, planteen el sistema de ecuaciones con el que se puede resolver el
siguiente problema.
Encontrar dos números tales que, el triple del primero
más el segundo es igual a 820. El doble del primero menos el segundo es igual
340.
Consigna 2: Resolver por el método de suma o resta los siguientes
sistemas de ecuaciones.
a) a + b = 135 b))
2m + 12n = -22
a - b =
59
8m – 12n =
32
Consigna 3: Resolver el siguiente problema:
Para el día del
estudiante los alumnos del grupo A compraron hamburguesas y refrescos. Un
equipo compró 5 hamburguesas y 3 refrescos y pagaron $235. Otro equipo compró,
a los mismos precios, 2 hamburguesas y 3 refrescos y pagaron $75. ¿Cuánto les
costó cada hamburguesa y cada refresco?
ACTIVIDAD 4:
Consigna 1. Organizados en equipos, planteen y resuelvan el sistema de
ecuaciones que resuelve el siguiente problema.
Diego y Claudia
fueron a una tienda de discos compactos. Diego fue al departamento de discos de
música y vio que todos estaban al mismo precio. Claudia fue al departamento de
películas y vio que todas estaban al mismo precio. Diego pagó $240 por dos
discos de música y una película; mientras que Claudia pagó $255 por un disco de
música y dos películas. ¿Cuál es el precio unitario de cada mercancía?
Consigna 2: Resuelve los siguientes sistemas de ecuaciones:
Consigna 3: Resolver los siguientes problemas.
a) Por cinco boletos para un concierto de rock
y tres boletos para un partido de fútbol
se pagaron $720 y por dos boletos para el mismo concierto y seis para el mismo
partido de fútbol se pagaron $480 ¿Cuál es el valor del boleto para cada uno de
los eventos?
b)
A un baile asistieron 270 personas. Si los boletos
de caballero costaban $100 y los de dama $80 y se recaudaron $24 800 por todas
las entradas, ¿cuántas mujeres y cuántos hombres asistieron al baile?
ACTIVIDAD 5: Consigna 1. Organizados en
equipos de tres resuelvan el siguiente problema:
Elena compró blusas y faldas, sabemos que el costo de
dos blusas equivale a 300 pesos menos el costo de 3 faldas y por otra parte
cada blusa cuesta veinticinco pesos más que cada falda ¿Cuanto cuesta cada
prenda?
Consigna 2: Resuelve los siguientes sistemas de ecuaciones:
ACTIVIDAD 6: Organizados en equipos de 3, revisen los
métodos de resolución de los problemas planteados y contesten las preguntas
argumentando sus respuestas.
Problema 1:
La suma de dos
números es 195. Si el doble del primer número menos el segundo es 60, ¿cuáles
son esos números?
Sistema:
x + y = 195
2x – y = 60
Simplificación:
x + y = 195
2x – y = 60
-----------------
3x
= 255
x = 255 / 3
x = 85
x + y = 195
85 + y = 195
y = 195 – 85
y = 110
a)
¿Por
qué creen que se eligió este método para resolver el sistema?
b)
Expliquen
con sus palabras en qué consiste el método utilizado.
Problema 2.
Dos hermanos ganan juntos $ 7,500.00 al mes. ¿Cuánto gana cada quien si
uno de ellos percibe $1,800.00 más que el otro?
8
Sistema:
a + b = 7500
b = a + 1800
Simplificación:
a + b = 7500
a + (a +´1800) =
7500
2a + 1800 = 7500
2a = 7500 – 1800
2a = 5700
a = 5700 / 2
a = 2850
b = a + 1800
b = 2850 + 1800
b = 4650
c)
¿Qué
método se utilizó al resolver este sistema de ecuaciones?
d)
¿Por
qué creen que se eligió este método?
e)
Expliquen
con sus palabras en qué consiste el método utilizado.
Problema 3:
Un vendedor de
frutas no recuerda el precio al que cobró las sandías y los melones; sólo sabe
lo siguiente:
|
Día
|
Venta
|
Conclusión
|
|
Lunes
|
Una sandía y
cuatro melones; cobró $ 49.00
|
La sandía cuesta
49 menos el precio de cuatro melones
|
|
Martes
|
Una sandía y
siete melones; cobró $ 73.00
|
La sandía cuesta
73 menos el precio de siete melones.
|
Según lo
establecido en la tabla ¿Cuál es el precio de cada una de las frutas?
Sistema:
s = 49 – 4m
s = 73 – 7m
49 – 4m = 73 – 7m
-4y + 7m = 73 – 49
3m = 24
m = 24 / 3
m = 8
s + 4m = 49
s + 4(8) = 49
9
s + 32 = 49
s = 49 – 32
s = 17
f)
¿Qué
método se utilizó al resolver este sistema de ecuaciones?
g)
¿Por
qué creen que se eligió este método?
ACTIVIDAD 7: Organizados
en equipos planteen un sistema de ecuaciones para cada uno de los problemas
siguientes y resuélvanlos utilizando el método algebraico que consideren conveniente.
- En
la cooperativa escolar se vendieron 296 refrescos en total. Si los
refrescos chicos vendidos fueron el triple de los medianos. ¿Cuántos se
vendieron de cada uno?
- La suma de dos números es 72 y su
diferencia es 48. ¿Cuáles son dichos números?
- Patricia
compró 10 estampillas de correos, unas de $3.00 y otras de $1.00. Si pago
$18.00 en total, ¿cuantos pagó por
cada una?
- Al
trabajar en un restaurante, Pedro ganó $37.00 más que Juan, pero si a lo
que ganó Juan se le restan $23.00,
la cantidad que se obtiene es $ 734.00. ¿Cuanto le corresponde a cada uno?
b) En un rectángulo, el doble del largo menos el
triple del ancho es 8 cm
y el triple del largo más el doble del ancho es 23cm. ¿Cuáles son las
dimensiones de dicho rectángulo?
a)
Dentro de cinco años, mi abuelito tendrá el cuádruplo
de mi edad. Hace cinco años tenía siete veces mi edad. ¿Qué edad tenemos él y
yo?
8.5.2 Tema 2.- SIMETRÍA AXIAL Y CENTRAL. ROTACIÓN Y TRASLACIÓN.
ACTIVIDAD 1: Consigna 1. Organizados
en parejas contesten las preguntas, con base en la información que ofrece el
siguiente dibujo
- uando
se habla de movimientos, hay dos que son muy conocidos, la rotación y la
traslación. ¿Cuál de ellos creen que se muestra en el dibujo?
___________________________
- ¿Cuál
es la medida del movimiento que se realizó? ________¿Cómo lo averiguaron?
_________________________________________________
- ¿Cuáles medidas del triángulo
ABC, que es la figura original, se conservan en el triángulo A’B’C’? __________________________________________
- ¿Cómo
son los lados homólogos de ambos triángulos?______________
Consigna
2. Individualmente,
realiza la traslación del polígono PQRST, considerando la directriz que se
marca. Nombra P’Q’R’S’T’ a la figura que trazaste.
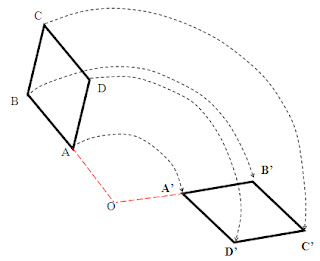
ACTIVIDAD 2: Consigna 1. Organizados
en parejas contesten las preguntas, con base en la información que ofrece el
siguiente dibujo
- Cuando
se habla de movimientos, hay dos que son muy conocidos, la rotación y la
traslación. ¿Cuál de ellos creen que se muestra en el dibujo?
___________________________
- ¿Cuál
es la medida del movimiento que se realizó? ________¿Cómo lo averiguaron?
_________________________________________________
- ¿Cuáles medidas del rombo ABCD,
que es la figura original, se conservan en el rombo A’B’C’D’?
__________________________________________
Consigna 2: Con sus
mismos compañeros comenten cuánto deben girar las siguientes figuras sobre su
centro para quedar en la misma posición y digan qué relación existe entre la
medida de ese ángulo y el ángulo central de la figura.
Consigna 3. De
manera individual efectúa la rotación de la siguiente figura.
a) ¿Cuántos grados gira la figura en cada movimiento? _______________
b) Al
tercer movimiento, ¿cuántos grados habrá girado la figura?__________
16
c) ¿Cuántos movimientos son necesarios
para que la figura A regrese a la
posición original?________________
ACTIVIDAD 3: Organizados en equipos, tracen la
imagen del triángulo ABC, considerando a “y” como eje de simetría y obtengan el
triángulo A’B’C’; enseguida reflejen esta figura tomando la recta “x” como eje
de simetría, para obtener la figura A’’B’’C’’.
Al finalizar, comenten mediante qué movimiento podrían obtener la figura
A’’B’’C’’ directamente de la figura ABC.
ACTIVIDAD 4: Organizados en equipos, hagan lo que se indica.
a)
Anoten
los valores que hacen falta en las tablas 2 y 3.
b)
Localicen
los puntos en el plano cartesiano y tracen las figuras.
c)
Verifiquen
que la figura que resulta de la tabla 2 es simétrica a la original con respecto
al eje y.
d)
Verifiquen
que la figura que resulta de la tabla 3 es simétrica a la que resulta de la
tabla 2, con respecto al eje x.
ACTIVIDAD 5: Organizados en equipos, hagan lo
siguiente:
a)
Tracen
el simétrico del triángulo ABC con respecto a la recta e, para obtener A’B’C’.
b)
Considerando
al eje w, reflejen el triángulo A’B’C’ y
obtengan el triángulo A’’B’’C’’.
¿Mediante qué movimiento y con qué medida se puede llegar del triángulo
ABC directamente al triángulo A’’B’’C’’? ___________________________
8.5.3 MANEJO DE LA INFORMACIÓN.
TEMA 4: SITUACIONES DE AZAR. EVENTOS EXCLUYENTES Y PROBABILIDAD DE OCURRENCIA
ACTIVIDAD
1: Las siguientes figuras
representan un tetraedro (poliedro regular de cuatro caras) y una ruleta. En
forma individual resuelve los problemas que se plantean y comenta tus
resultados con tres de tus compañeros más cercanos.
1.- Al girar la ruleta, ¿qué probabilidad existe de
que la ruleta se detenga en...
a)
el
número 5?
b)
un
número menor que 4?
c)
un
múltiplo de 2?
d)
un
número impar?
2.- Si se lanza el tetraedro, ¿cuál es la
probabilidad de que la cara que quede sobre la superficie plana, sea…
a)
color
rojo?
b)
verde
o rojo?
c)
verde
o blanco o rojo?
ACTIVIDAD
2: Consigna 1. El
experimento consiste en girar la ruleta de la sesión anterior y observar en qué
número se detiene. Con base en esto contesten en equipo las siguientes
preguntas:
a)
¿Cuál
es la probabilidad de que la ruleta se detenga en un número par?
b)
¿Cuál
es la probabilidad de que la ruleta se detenga en un número impar?
c)
¿Pueden
ocurrir al mismo tiempo los eventos a) y b)?, ¿porqué?
d)
¿Cuál
es la probabilidad de que la ruleta se detenga en un número par o un número
impar?
a)
¿Cuál
es la probabilidad de que la ruleta se detenga en un número par o
múltiplo de tres?
b)
¿Cuál
es la probabilidad de que la ruleta se detenga en un número par y
múltiplo de tres?
Consigna 2: Con el mismo equipo resuelvan el siguiente
problema. Se hace referencia al tetraedro y ruleta de la sesión anterior.
Se lanza el
tetraedro y se hace girar la ruleta simultáneamente, ¿qué probabilidad hay de
que la ruleta se detenga en el número 4 y el tetraedro caiga sobre su color
verde?
ACTIVIDAD
3: Resuelvan en equipos los
siguientes problemas. Se hace referencia a la ruleta de las sesiones
anteriores.
1.
Si se
tienen los eventos:
- Que la ruleta se
detenga en un número menor que cuatro.
- Que se detenga en un
número múltiplo de cuatro.
a) ¿Cuál es
la probabilidad del evento A? p(A) =
___________
b) ¿Cuál es
la probabilidad del evento B? p(B) =
___________
c) ¿Qué
significa que ocurra A o B?___________________________________
d) ¿Cuál es la probabilidad de que ocurra A o
B? p(A o B) = ______________
Expliquen su respuesta.
2. Ahora se tienen los eventos siguientes:
- Que la ruleta se
detenga en un número mayor que cuatro.
- Que la ruleta se
detenga en un múltiplo de cuatro.
a) Obtengan: p(C) = __________ p(D) = ____________
b) ¿Cuál es la probabilidad de que ocurra C o
D? P(C o D) = ____________
3. Comparen los resultados de d) del ejercicio 1 y
de b) del ejercicio 2 y comenten las formas de obtenerlos.
¿Existe alguna diferencia en estos eventos? ¿Cuál?
ACTIVIDAD 4. Organizados en equipos,
resuelvan el siguiente problema:
Se tienen dos dados, uno
azul y otro rojo, que tienen sus caras marcadas con puntos del uno al seis. El
experimento consiste en lanzar simultáneamente los dos dados. Los resultados
posibles del experimento son parejas de números en los cuales el primero es el
número de puntos del dado rojo y el segundo del azul. Completen la tabla.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a) ¿Cuántos resultados posibles tiene el experimento?
________________
b) ¿Cuál es la probabilidad de que ocurra cada uno de
ellos? ____________
c) Anoten los resultados que hacen falta en la
siguiente tabla.
|
EVENTO
|
RESULTADOS POSIBLES
|
PROBABILIDAD
|
|
A {La suma es dos}
|
|
|
|
B {La suma es tres}
|
|
|
|
C {La suma es siete}
|
6
|
6/36
|
|
D {La suma es diez}
|
|
|
|
E {La suma es 3 o 10}
|
|
|
|
F {La suma es mayor que 10 o múltiplo de 4}
|
|
|
d) ¿Qué evento tiene mayor
probabilidad? _______________
a)
¿Qué evento tiene menor probabilidad? _______________
b)
Formulen un evento compuesto por dos eventos que sean
mutuamente excluyentes. _________________________________
c)
Formulen un evento compuesto por dos eventos que NO sean
mutuamente excluyentes. _________________________________
Suscribirse a:
Comentarios (Atom)